Daniel Tubbenhauer on Mahler's Theorem

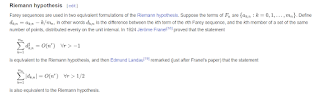
This is an almost mechanical way to prove that certain types of recursively defined functions generate transcendental numbers. See Toby: "Locked in a school bus until I learn what fractals are" where I suggested that it would be interesting to consider the sets generated by Edmund Landau's 1934 Riemann Hypothesis equivalent in Daniel Tubbenhauer and Holly Krieger on The Riemann Hypothesis.

See Farey sequence and also Bill Gosper's Dragon Curves, which are related to this sequence: Bill Gosper, Continued Fractions and The Dragon Curve. 

I think what we are showing here is how much more fun, and how much easier it is to understand mathematics when you talk with one another, without holding on to all your really good ideas until you have time to mine them for your own personal glory, because there are so many ideas out there that nobody will ever have time to exploit more than just a few of them, unless we start building mathematics in a sane, logically sound manner so that we can understand better the real relations between the different concepts that emerge through this process. We are not only in a post-scarcity world materially and energetically, but intellectually as well. Wake up people!

Subscribe to Daniel Tubbenhauer.

Comments

Post a Comment

Popular posts from this blog

Live Science - Leonardo da Vinci's Ancestry

Image
... and his posterity too? See  On Communication in Linear Time And Hypertext And The Gospel of Sophia . So it looks like El Cielo of the cistine [sic!😂] chapel is not the limit anymore.  I think I just met one of his descendents. A guy called Versailles Toledo who is from Chiapas. That might explain the murals I mention in my recent untitled post , just before the post mentioning this video. I also just took this photo of Rafael Gonzales, born here in Tecate, B.C., who told me about a spring near here called Agua Fría , half way from Tecate to Loma Tova , where, a few decades ago, people used to go to have barbecues and stuff, but now he thinks it may be private land. If someone reading this has a Facebook account, please write a link to this post onto his FB page. To see why I took the photo, look at his T-shirt and the horse-shoes and ponder this: Subscribe to BeatrizER and her video(s?) about mathematical logic, ... Sounds like Edith (II) Rix has been online all the time, ...
Read more

David Turner Obituary by Sarah Nicholas Fri 24 Nov 2023

Image
This was in The Guardian: David Turner obituary , only eight days after I posted  David Turner Talking About Sixty Years of Functional Programming History : This talk was given in London in 2017: See  Turner, D. A. "Some History of Functional Programming Languages" also  John Hughes - Why Functional Programming Matters  and David MacQueen's talk at ICFP 2015 in  Numberphile - Sophie Maclean on the Catalan Numbers . At 10:30 This whole discussion abut combinator reduction is especially interesting. I didn't know Arthur Norman had tried building hardware for combinator machines. I'll look that up: maybe start here A.C. Norman  Faster combinator reduction using stock hardware  in LFP '88: Proceedings of the 1988 ACM conference on LISP and functional programming. At 26:25 on the ISWIM virtual machine implemented in the PAL compacting garbage collector?! This work Reynolds and others did was at MIT in Masecheusetts and Argonne National Laboratory Illinois. Did
Read more